Unveiling the Enigma: What is Pi Worth and Why Does It Matter?

Pi (π), the mathematical constant representing the ratio of a circle’s circumference to its diameter, is far more than just a number. Its seemingly simple definition belies its profound implications across mathematics, physics, engineering, and even everyday life. So, what is pi worth? Its value is approximately 3.14159, but its decimal representation continues infinitely without repeating. This irrational nature makes it both fascinating and crucial for various calculations and applications.

This article delves into the history, significance, and applications of pi, exploring why understanding pi worth is essential for grasping fundamental concepts in science and technology. We’ll examine its role in everything from calculating the volume of a sphere to powering advanced algorithms in computer science.

The History of Pi: A Journey Through Time

The concept of pi has captivated mathematicians for millennia. Ancient civilizations, including the Babylonians and Egyptians, recognized the relationship between a circle’s circumference and diameter. They developed approximations of pi worth that, while not perfectly accurate, were remarkably close considering the limited mathematical tools available at the time.

• Babylonians: Around 1900-1680 BC, they approximated pi as 3.125 (3 1/8).
• Egyptians: The Rhind Papyrus (c. 1650 BC) suggests an approximation of pi as (16/9)² ≈ 3.1605.
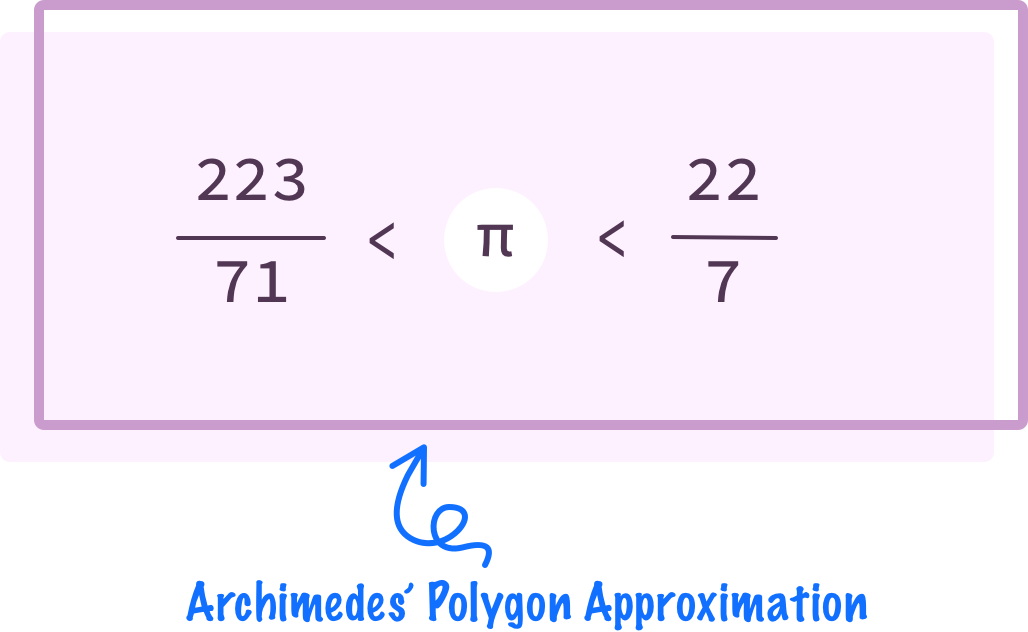
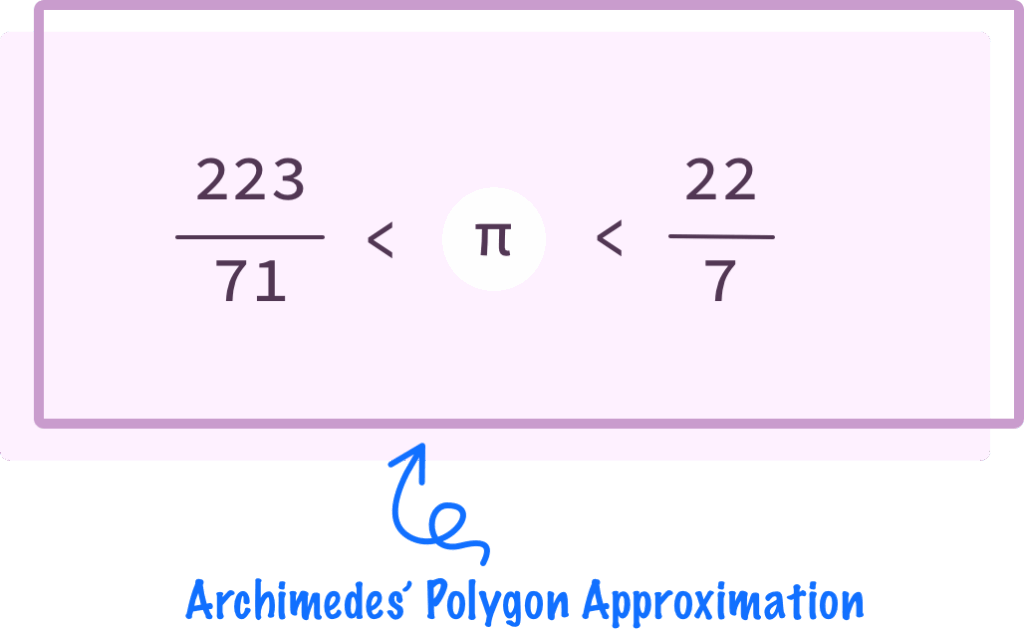
• Archimedes: The Greek mathematician Archimedes (c. 250 BC) used polygons inscribed and circumscribed within a circle to more accurately estimate pi worth, arriving at a value between 3 1/7 (≈ 3.1429) and 3 10/71 (≈ 3.1408).

Over centuries, mathematicians refined their methods for calculating pi worth. In the 17th century, the development of calculus provided powerful new tools for calculating pi to unprecedented levels of accuracy. [See also: History of Mathematical Constants] Mathematicians like Isaac Newton and Gottfried Wilhelm Leibniz made significant contributions to the field.

The Significance of Pi: Beyond the Circle

While pi worth is defined in terms of circles, its significance extends far beyond geometry. It appears in numerous formulas and equations across various scientific disciplines. Understanding its importance is crucial for anyone studying mathematics, physics, or engineering.

Pi in Mathematics

Pi is fundamental to many areas of mathematics, including:

• Geometry: Calculating the area and circumference of circles, the volume and surface area of spheres and cylinders.
• Trigonometry: Pi is used to define angles in radians, a standard unit of angular measurement. Trigonometric functions like sine, cosine, and tangent are periodic with a period of 2π.
• Calculus: Pi appears in integrals, derivatives, and infinite series. For example, the Leibniz formula for π states that π/4 = 1 – 1/3 + 1/5 – 1/7 + …
• Number Theory: Though an irrational number, pi is related to fundamental concepts in number theory.

Pi in Physics

Pi worth also plays a crucial role in various physics applications, including:

• Electromagnetism: Pi appears in Maxwell’s equations, which describe the behavior of electric and magnetic fields.
• Quantum Mechanics: Pi appears in the Heisenberg uncertainty principle and the Schrödinger equation, which are fundamental to understanding the behavior of subatomic particles.
• General Relativity: Pi is used in Einstein’s field equations, which describe the relationship between spacetime and gravity.
• Fluid Dynamics: Calculations involving circular pipes and fluid flow rely on the accurate value of pi worth.

Pi in Engineering

Engineers rely on an accurate understanding of pi worth for a wide range of applications, such as:

• Civil Engineering: Designing circular structures like bridges, tunnels, and water tanks requires precise calculations involving pi.
• Mechanical Engineering: Calculating the volume and surface area of cylindrical and spherical components in machines and engines.
• Electrical Engineering: Analyzing alternating current (AC) circuits, which involve sinusoidal functions that depend on pi.
• Aerospace Engineering: Designing aircraft and spacecraft, where aerodynamic calculations often involve circular and spherical shapes.

Calculating Pi: From Ancient Methods to Modern Algorithms

Over the centuries, mathematicians have developed increasingly sophisticated methods for calculating pi worth to ever-greater accuracy. From the geometric approximations of Archimedes to the infinite series formulas of the 17th century, the quest to determine pi has driven mathematical innovation.

Archimedes’ Method

As mentioned earlier, Archimedes used inscribed and circumscribed polygons to approximate the circumference of a circle. By increasing the number of sides of the polygons, he obtained increasingly accurate estimates of pi worth. This method, while computationally intensive, was a significant breakthrough for its time.

Infinite Series

The development of calculus in the 17th century led to the discovery of infinite series formulas for pi. These formulas, such as the Leibniz formula mentioned earlier, allowed mathematicians to calculate pi worth to a much higher degree of accuracy. However, many of these series converge slowly, requiring a large number of terms to achieve a desired level of precision.

Modern Algorithms

Modern algorithms, such as the Chudnovsky algorithm, are significantly more efficient than earlier methods. The Chudnovsky algorithm, developed in the late 20th century, is based on advanced mathematical concepts and can calculate pi worth to trillions of digits. These algorithms are typically implemented on high-performance computers and require significant computational resources.

The Irrationality and Transcendence of Pi

One of the most fascinating aspects of pi is its irrationality and transcendence. An irrational number cannot be expressed as a fraction of two integers. A transcendental number is not the root of any non-zero polynomial equation with rational coefficients. In other words, pi worth cannot be expressed as a simple fraction and is not the solution to any algebraic equation.

The irrationality of pi was first proven in 1761 by Johann Heinrich Lambert. The transcendence of pi was proven in 1882 by Ferdinand von Lindemann. These proofs established that pi is fundamentally different from rational numbers and algebraic numbers, further solidifying its unique place in mathematics.

Pi in Popular Culture

The constant pi has permeated popular culture, celebrated in various ways beyond its mathematical significance. Pi Day, observed annually on March 14th (3/14), is a popular celebration among mathematicians, scientists, and math enthusiasts. People often commemorate the day by eating pie, reciting digits of pi, and engaging in mathematical activities.

Pi worth has also appeared in literature, film, and music. Its infinite nature and mysterious properties have inspired artists and writers for generations. The movie “Pi,” directed by Darren Aronofsky, explores the obsession with finding patterns and meaning in the universe through the lens of a mathematician searching for a hidden code in pi.

Practical Applications of Knowing Pi Worth

While calculating pi to trillions of digits might seem like an abstract exercise, there are practical applications for knowing pi worth to a high degree of accuracy. These applications include:

• Scientific Research: Accurate calculations involving pi are essential for research in physics, astronomy, and other scientific disciplines.
• Computer Simulations: Many computer simulations, such as those used in weather forecasting and climate modeling, rely on precise calculations involving pi.
• Cryptography: Pi is used in some cryptographic algorithms.
• Engineering Design: As mentioned earlier, engineers rely on pi for designing a wide range of structures and machines.

The Future of Pi Research

Despite centuries of research, the study of pi continues to be an active area of mathematical inquiry. Mathematicians are still exploring the properties of pi and searching for new and more efficient ways to calculate its value. [See also: Unsolved Problems in Mathematics] The quest to understand pi worth is not just about calculating digits; it’s about gaining deeper insights into the fundamental nature of numbers and the universe.

One area of ongoing research is the search for patterns in the digits of pi. While pi is known to be an irrational number, it is still unknown whether its digits are normally distributed. This means that each digit (0-9) would appear with equal frequency in the infinite decimal expansion of pi. Determining whether pi is normal is a challenging problem that has implications for our understanding of randomness and chaos.

Conclusion

Pi worth, seemingly a simple ratio, holds profound implications across mathematics, science, and engineering. From ancient approximations to modern algorithms, the quest to understand pi has driven mathematical innovation and provided essential tools for solving complex problems. Whether you’re calculating the circumference of a circle or designing a spacecraft, an accurate understanding of pi is crucial. Its irrational and transcendental nature continues to fascinate mathematicians and inspire artists, making pi a truly remarkable constant.